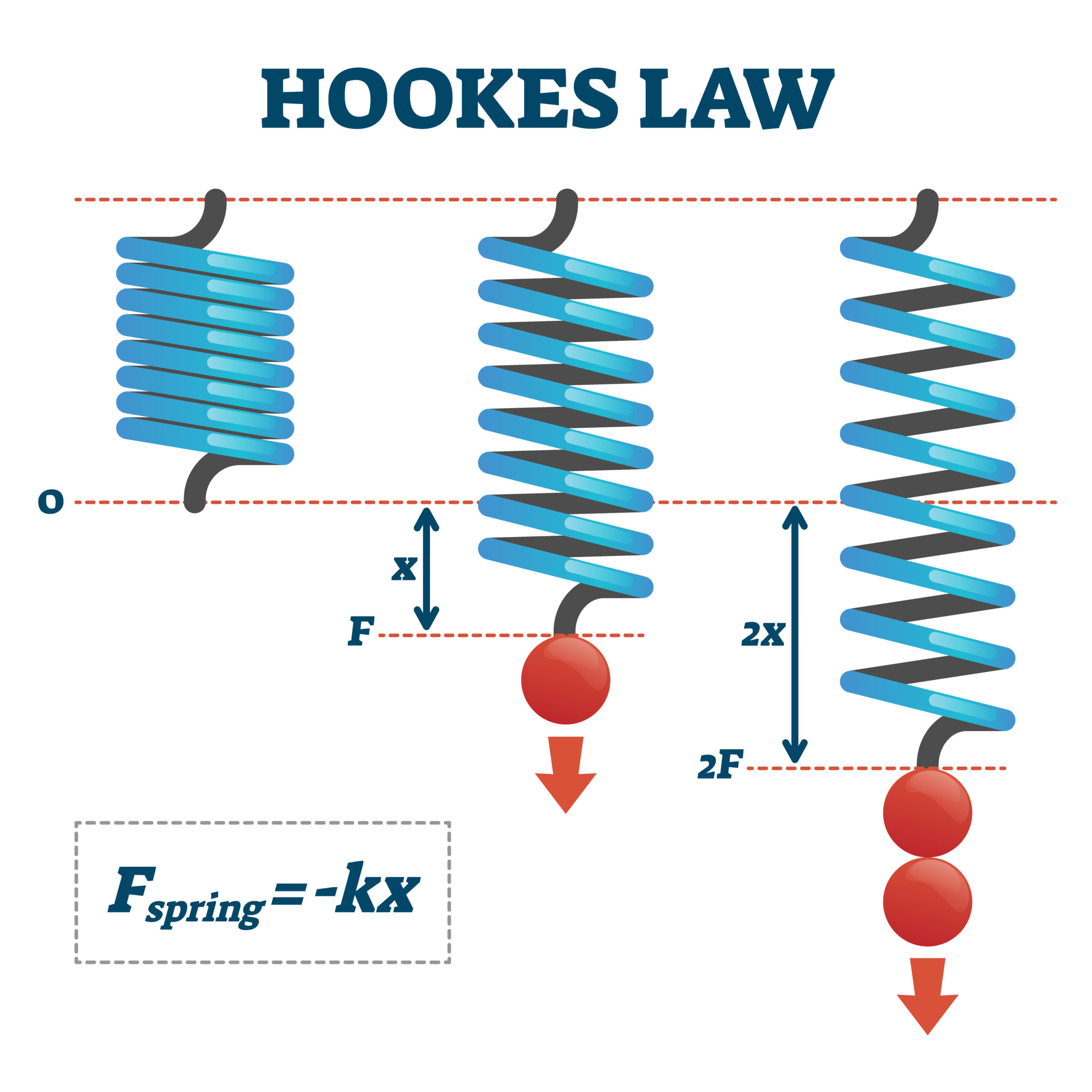
Hooke’s Law states that the force (F) required to extend or compress a spring by some distance (x) is directly proportional to that distance. The constant of proportionality is known as the spring constant (k). The mathematical equation for Hooke’s Law is F = kx. This equation holds true as long as the spring is stretched or compressed within its elastic limit, beyond which it will become permanently deformed.

Hooke’s Law is a fundamental principle in the field of physics and engineering, particularly in the study of elasticity and mechanics. It was first stated by Robert Hooke in 1678, although it had been observed by others before him. The law applies to a wide range of materials and structures that exhibit elastic behavior, including not only springs but also rods, beams, and membranes.

The spring constant (k) is a measure of the spring’s stiffness, and it depends on the material and geometry of the spring. A spring with a larger spring constant requires more force to be stretched or compressed the same distance than a spring with a smaller spring constant.

The elastic limit of a spring is the maximum amount of stress (force per unit area) that the spring can withstand before it becomes permanently deformed. The elastic limit is different for different materials and also depends on the geometry and size of the spring.

In addition to its applications in mechanics, Hooke’s Law has many practical uses in engineering, such as in the design of bridges, buildings, and vehicles. It is also used in the analysis of vibrations and wave propagation in structures, and in the study of the mechanical behavior of biological tissues.

It’s worth noting that Hooke’s Law is limited to elastic deformation, and it’s not applicable for plastic deformation. When the material exceeds its elastic limit and starts to deform plastically, the stress-strain curve deviates from the linearity and the proportionality of the force and deformation no longer holds.

Statement of Hooke’s Law

The statement of Hooke’s Law is a fundamental principle in the field of physics and engineering, which describes the relationship between the force applied to an elastic object, and the resulting displacement or deformation of that object. The law states that the force required to stretch or compress an elastic object, such as a spring, is proportional to the amount of stretch or compression. The proportionality constant is known as the spring constant, k.

Mathematically, Hooke’s Law can be expressed as: F = kx, where F is the force applied, k is the spring constant, and x is the displacement or deformation of the object caused by the force. This equation holds true as long as the object is stretched or compressed within its elastic limit. The elastic limit is the maximum amount of stress that an object can withstand before it becomes permanently deformed.

It’s important to note that Hooke’s Law applies to any elastic object such as a spring, rod, beam, or membrane, and it holds true for all linear elastic materials such as metals, polymers, rubber, and most biological tissues. But it’s limited to elastic deformation and it’s not applicable for plastic deformation, where the material exceeds its elastic limit and starts to deform plastically, the stress-strain curve deviates from the linearity and the proportionality of the force and deformation no longer holds.

In practical applications, Hooke’s Law is widely used in the design and analysis of a wide range of mechanical systems, including bridges, buildings, vehicles, and many other structures. It’s also used in the study of vibrations, wave propagation, and the mechanical behavior of biological tissues.

Equation of Hooke’s Law

The equation of Hooke’s Law is:

F = kx

Where:

• F is the force applied (measured in newtons, N)
• k is the spring constant (measured in newtons per meter, N/m)
• x is the displacement or deformation caused by the force (measured in meters, m)

This equation states that the force (F) required to extend or compress a spring by some distance (x) is directly proportional to that distance, as long as the spring is stretched or compressed within its elastic limit. The proportionality constant is the spring constant (k) which is a measure of the spring’s stiffness and depends on the material and geometry of the spring. The greater the spring constant, the more force is required to stretch or compress the spring the same distance.

It’s worth noting that Hooke’s Law is limited to elastic deformation and not applicable for plastic deformation. When the material exceeds its elastic limit and starts to deform plastically, the stress-strain curve deviates from the linearity and the proportionality of the force and deformation no longer holds.

Graphs of Hooke’s Law

Graphs of Hooke’s Law typically show the relationship between the force applied to an elastic object and the resulting displacement or deformation of that object. The graph is a straight line, with the force on the y-axis and the displacement on the x-axis. The slope of the line is equal to the spring constant (k), and the y-intercept is zero, as there is no displacement when the force is zero.

When a force is applied to a spring within its elastic limit, the spring will stretch or compress and the graph will be a straight line. The slope of the line will be equal to the spring constant (k) of the spring.

If a force is applied to the spring beyond its elastic limit, the spring will not return to its original shape and size. The graph would deviate from the linearity, and the proportionality of the force and deformation no longer holds.

It’s important to note that Hooke’s Law applies to any elastic object such as a spring, rod, beam, or membrane, and it holds true for all linear elastic materials such as metals, polymers, rubber, and most biological tissues, the graphs would be similar but the spring constant would be different depending on the material and geometry.

Applications of Hooke’s Law

Hooke’s Law has many practical applications in engineering and physics, some examples are:

• Mechanical Engineering: Hooke’s Law is used in the design of mechanical systems such as bridges, buildings, vehicles, and other structures. It is used to determine the forces and displacements in these systems, and to ensure that they can withstand the loads they are expected to encounter.
• Vibration Analysis: Hooke’s Law is used to analyze the vibrations of mechanical systems, such as machines and structures. By understanding how a system responds to different forces, engineers can identify potential problems and take steps to prevent them.
• Wave Propagation: Hooke’s Law is used to study the propagation of waves in elastic materials, such as sound waves in air and seismic waves in the Earth. By understanding how these waves travel through materials, scientists can better predict and respond to natural disasters such as earthquakes.
• Biomechanics: Hooke’s Law is used to study the mechanical properties of biological tissues, such as bones, muscles, and tendons. By understanding how these tissues respond to different loads, scientists can better understand and treat injuries and diseases.
• Materials Science: Hooke’s Law can be used to analyze the mechanical properties of materials. By measuring the stress-strain curve of a material, scientists can determine its elastic modulus, which is a measure of a material’s stiffness and is used to predict how a material will behave under different loads.
• Industrial applications: Hooke’s Law is widely used in the design and optimization of many industrial applications such as springs, shock absorbers, and vibration dampers.

It’s worth noting that Hooke’s Law is limited to elastic deformation and not applicable for plastic deformation, but it’s a fundamental principle that helps to understand the behavior of many systems, and it’s widely used in the design, analysis and optimization of many mechanical systems.

Limitations of Hooke’s Law

Hooke’s Law is a fundamental principle that describes the behavior of elastic materials and structures, but it has some limitations:

1. Elastic limit: Hooke’s Law is only valid for forces applied within the elastic limit of a material or structure. Once a material exceeds its elastic limit, it will become permanently deformed and the proportionality between force and deformation no longer holds.
2. Linearity: Hooke’s Law is based on the assumption of linearity, meaning that the relationship between force and deformation is a straight line. In reality, the relationship between force and deformation can be more complex, especially in materials that exhibit nonlinear behavior, such as rubber and some polymers.
3. Temperature: Hooke’s Law assumes that temperature is constant and does not affect the spring constant or the elastic limit of the material. In reality, temperature changes can affect the spring constant and the elastic limit of a material, leading to changes in the behavior of the material.
4. Dynamic loading: Hooke’s Law assumes that the loading is static and the material is at rest. In dynamic loading, the material is subjected to time-varying loads, and the behavior of the material is different.
5. Creep and relaxation: Hooke’s Law is based on the assumption that the deformation is instantaneous and the material returns to its original shape when the force is removed. But in some materials, the deformation is not instantaneous and the material does not return to its original shape, this behavior is called creep and relaxation.
6. Inelastic behavior: Hooke’s Law is limited to elastic deformation and not applicable for plastic deformation, where the material exceeds its elastic limit and starts to deform plastically, the stress-strain curve deviates from the linearity and the proportionality of the force and deformation no longer holds.

Despite these limitations, Hooke’s Law remains a fundamental principle in the field of physics and engineering and is widely used in the design, analysis, and optimization of many mechanical systems.